Maths and Science tuition made easy, one-to-one home tuition
Maths and Science tuition made easy, one-to-one home tuition
The Academy of Sciences theacademyofsciences.co.uk
Completing the square
To understand the principle of completing the square you have to be familiar with the perfect square which when multiplied out gives the square of the two terms (inside the bracket x and a) and twice their product (2ax). This is shown below:
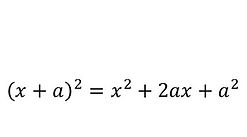
This can be rearranged to give:
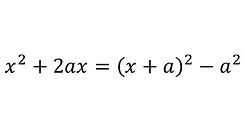
This is the basic principle of completing the square for an expression that is not quite a perfect square (expression on the left of the equation).
Notice the relationship between the expression and the completed square.
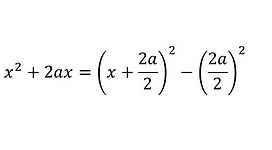
This can be rewritten as a formula by replacing 2a = b where b is a number:
Completing the square for expressions of the form:
Where a is a number.
Example 1
Example 2
Exercise 1
Complete the square for the following expressions:
Completing the square for expressions of the form:
Example 1
Example 2
Exercise 2
Complete the square for the following expressions:
Solving quadratic equations by completing the square
Quadratic equations can be solved by firstly completing the square and then simple re-arrangement as shown in the example below:
Example 1
x² - 6x - 2 = 0
Firstly complete the square as in the previous examples, so:
x² + 6x - 2
= (x + 3)² - 3² - 2
= (x + 3)² - 9 - 2
= (x + 3)² - 11
As the original quadratic equation was equal to zero, the completed square is also equal to zero.
(x + 3)² - 11 = 0
Now re-arrange to make x the subject and you will have solved it. Firstly take the 11 over to the right hand side.
(x + 3)² = 11
Square root both sides to eliminate the bracket.
x + 3 = ±√11
Finally take 3 to the right hand side and you have solved the equation.
= -3 ±√11
Note: when you square root a number you get both the positive and negative values of the root.
The solution can be left as a surd as above if the question specifically states this otherwise it will have to be given as a normal number.
Example 2
Solve the following equation by completing the square and leaving the answer in surd form.
x² - 4x - 7 = 0
x² - 4x - 7
= (x - 2)² - 2² - 7
= (x - 2)² - 4 - 7
= (x - 2)² - 11
(x - 2)² - 11 = 0
x - 2 = ±√11
x = 2 ±√11
Exercise 3
Solve the following equations by completing the square and leaving the answer in surd for where appropriate.
1. x² + 8x - 3 = 0
2. x² + 6x + 5 = 0
3. x² + 4x - 7 = 0
4. x² - 5x - 5 = 0
5. x² + 14x - 1 = 0
6. x² + 10x - 7 = 0
7. x² - 12x - 3 = 0
8. x² + 2x - 5 = 0
9. x² + 16x - 3 = 0
10.x² - 20x - 3 = 0